An introduction to graph embeddings and why they are valuable

From networks of fraudsters to social networks to international supply chains, graphs capture the essence of complex networks of relationships. Graph structures have emerged as a powerful tool for representing and analyzing interconnected information. 

But working with graph data can present certain challenges, particularly when it comes to applying machine learning techniques. This is where graph embeddings come in. Graph embeddings let you translate the rich information contained in graphs into a format that's both mathematically tractable and computationally efficient.

In this article, we'll explore what graph embeddings are, how they work, and some of the applications where they are most valuable. By the end, you'll understand why graph embeddings are an important tool in the data scientist's toolkit for tackling complex, interconnected data problems by combining graph analytics and machine learning.

Before diving into graph embeddings, let's briefly review what a graph is. A graph is a mathematical structure consisting of nodes (also called vertices) and edges (also called relationships). Nodes represent individual entities, while edges represent the connections between these entities. What sets graphs apart from other data representations is their ability to explicitly model and store these relationships, making them ideal for representing complex, interconnected systems.

Graph analytics in and of itself is already quite powerful for detecting complex patterns using graph algorithms and providing visual context to analysis. The functionalities of graph and machine learning complement each other. Graph data can be ingested into machine learning algorithms, and then be used to perform classification, clustering, regression, etc. Together, graph and machine learning provide greater analytical accuracy and faster insights. 

Graph also increases the explainability of machine learning. It can demonstrate why an AI system arrived at a certain decision, for example assigning a specific risk score to a particular loan applicant.

Graph embeddings are a way to translate the structural information of a graph into a compact vector representation. Graph embeddings map each node of a graph to a low-dimensional vector space while preserving the graph's structural properties. These vectors, typically real-valued and dense, capture the essence of a node's position and role within the broader network structure.

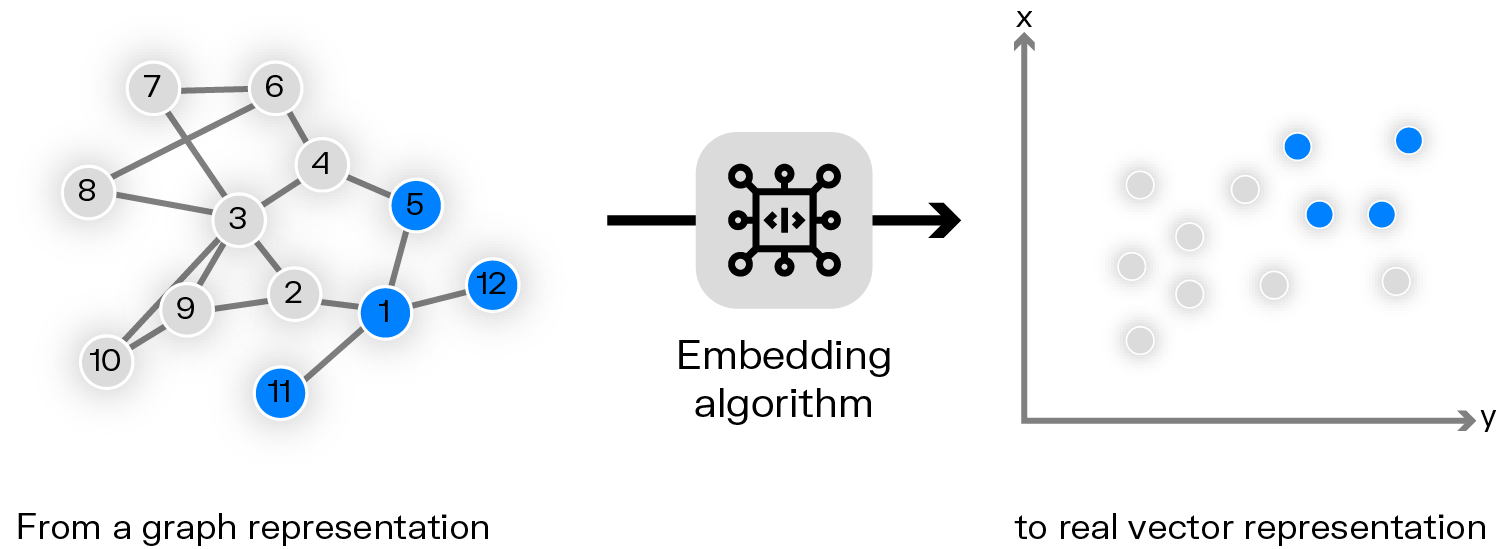
The concept behind graph embeddings is to create a representation where nodes that are similar or closely connected in the original graph are also close to each other in the embedded vector space. This transformation allows you to apply various machine learning algorithms that work well with vector inputs but struggle with graph-structured data.

Graph embeddings enable you to enhance certain functionalities of graph, and integrate with other technologies. The value of graph embeddings lies in several key aspects:

1. Capturing interconnectedness: The primary strength of graph embeddings is their ability to encapsulate the underlying interconnectedness of a graph. This is crucial because the very power of graph data in analytics comes from these complex relationships. By preserving this structural information in a vector format, you maintain the essence of what makes graph data so valuable.
2. Compatibility with machine learning: Graph embeddings act as a bridge between graph-structured data and traditional machine learning algorithms. By translating graph relationships into numerical vectors, you open up a vast array of machine learning techniques that can now be applied to graph data. 
3. Dimensional reduction: Graphs, especially very large ones, can be high-dimensional, with each node potentially connected to many, many others. Graph embeddings tend to reduce this to a much lower-dimensional space (often in the range of tens to hundreds of dimensions). This reduction improves computational efficiency and helps in mitigating the challenge of dimensionality, a common issue in machine learning with high-dimensional data.
4. Uncovering hidden relationships: One of the most exciting aspects of graph embeddings is their ability to reveal hidden relationships within the data. The embedding process can uncover patterns and similarities between nodes that might not be immediately apparent in the original graph structure. This can lead to new insights and discoveries, particularly in complex networks where direct relationships may obscure more subtle, higher-order connections.

Graph embeddings are created through algorithms that aim to preserve the structural properties of the graph in a lower-dimensional vector space. The process involves mapping each node to a vector of real numbers, typically in a space with far fewer dimensions than the original graph structure.

At a high level, the calculation of graph embeddings involves optimizing an objective function that balances two main goals:

1. Proximity preservation: Nodes that are close or similar in the original graph structure should have similar vector representations in the embedded space.
2. Structural equivalence: Nodes that play similar roles in the graph (e.g. having similar neighborhood structures) should have similar embeddings, even if they're not directly connected.

The specific methods for achieving these goals vary depending on the algorithm used, but they often involve techniques like random walks, matrix factorization, etc.

There are numerous algorithms for creating graph embeddings, each with its own strengths and particular use cases. Let's explore three popular graph embedding algorithms:

DeepWalk applies ideas from natural language processing (NLP) to graph embeddings. It performs random walks on the graph to generate sequences of nodes, and treats these sequences as if they were sentences in a language, providing context around each node.

DeepWalk is particularly effective in real world applications such as network classification and anomaly detection.

Node2Vec is an extension of DeepWalk that offers more flexibility in exploring graph neighborhoods. Node2Vec allows for capturing both homophily (nodes with similar connections are close) and structural equivalence (nodes with similar structural roles are close).

Node2Vec is versatile and can be tuned to capture different aspects of network structure, making it suitable for a wide range of applications.

GraphSAGE takes a different approach by learning a function to generate embeddings rather than learning individual embeddings. Its process includes sampling and aggregating features from a node's local neighborhood, using these aggregated features to generate the node's embedding, and employing various aggregate functions to combine neighbor information.

GraphSAGE is particularly useful for large graphs and can generate embeddings for unseen nodes, making it suitable for dynamic or growing graphs.

Each of these algorithms approaches the task of creating graph embeddings differently, but they all aim to capture the essential structural information of the graph in a compact, vector format. The choice of algorithm depends on the specific characteristics of the graph, the desired properties of the embeddings, and the downstream task for which the embeddings will be used.

The process of creating graph embeddings often involves experimentation with different algorithms and hyperparameters to find the approach that best captures the relevant aspects of the graph structure for the task at hand.

Graph analytics on its own is already powerful, but graph embeddings can help enhance those capabilities. Graph embeddings can be applied across various domains due to their ability to capture complex relational information in a format favorable to other advanced analytical techniques. Let's take a look at three key applications of graph embeddings for enhancing graph analytics.

Graph embeddings serve as a bridge between graph-structured data and traditional machine learning algorithms. By transforming graphs into vector representations, you can bridge the gap and apply a wide range of machine learning and deep learning techniques that typically work with tabular or vector data. Some notable applications include:

• Node classification, which predicts the labels or categories of nodes in a graph. In a social network, for example, this could involve identifying user interests or demographics based on their connections and interactions.
• Clustering, which groups similar nodes or subgraphs together. This can be applied in community detection in social networks or identifying functional modules in biological networks.
• Anomaly detection, identifying nodes, edges, or subgraphs that deviate significantly from the norm. This is particularly useful in fraud detection or network security applications.

Another application of graph embeddings is the ability to quantify similarity between nodes in a graph. Since embeddings represent nodes as vectors in a continuous space, you can use various distance or similarity metrics to compare them. Applying similarity measures enables various downstream tasks:

• Recommendation systems for e-commerce or content platforms, where similarity between user or item embeddings can drive personalized recommendations. (See our article on graph and machine learning for a closer look at this use case.)
• Information retrieval: Finding similar documents or web pages based on their graph representations.
• Knowledge graph completion: Identifying similar entities to fill in missing information in knowledge graphs.

The ability to quantify node similarity opens up numerous possibilities for analyzing and leveraging complex network structures across diverse domains.

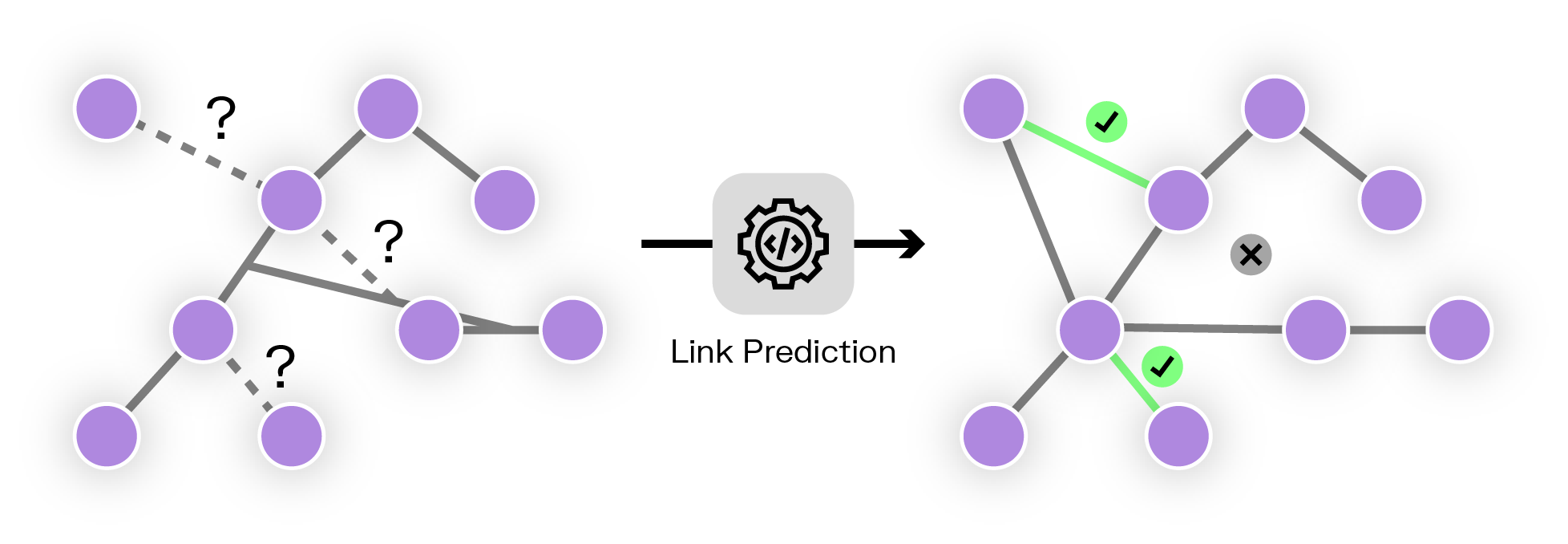
Link prediction is a fundamental task in network analysis, used to forecast additional edges in a graph. Graph embeddings are particularly effective for this task. Combining embedding vectors with a supervised classifier lets you predict where you might add new relationships within your graph.

Link prediction has a number of applications, including:

• Social networks: Suggesting new connections or friendships to users.
• Bioinformatics: Predicting protein-protein interactions or gene-disease associations.
• E-commerce: Forecasting potential customer-product interactions for targeted marketing.
• Cybersecurity: Anticipating potential attack vectors in computer networks.

The power of graph embeddings in link prediction lies in their ability to capture both local and global graph structure, allowing for more nuanced and accurate predictions compared to methods that rely solely on direct connections or simple graph statistics.

Graph embeddings are a versatile tool with applications spanning machine learning, similarity measurement, and network prediction tasks. By translating the rich, relational information of graphs into a format compatible with a wide array of analytical techniques, graph embeddings enable new insights and capabilities across diverse fields. As research in this area continues to advance, we can expect to see even more innovative applications leveraging the power of graph embeddings to tackle complex, interconnected data challenges.